优先支付自己是实现持续投资的重要法则。
长期复利是财富积累的秘密,投资要趁早。

 从时间的角度思考投资
从时间的角度思考投资
|
你会依据直觉来投资吗?多数人在投资之前希望掌握合理投资的基本原则。在介绍基本投资选择和重要的投资原则之前,我们先来做一个练习。
货币的时间价值 你也许听说过《存在与时间》,这是一部艰深的著作。大多数人没有勇气去读它,但即使你从未听说过这本书,也不会影响自己的生活。然而,对于任何有兴趣投资的人,如果不理解投资与时间的关系,她将很难取得投资的成功。 当前所持有的一定量的货币,比未来获得的等量货币具有更高的价值,这种现象称为货币的时间价值。货币之所以表现出时间价值,是因为:
单利与复利 单利与复利是计算货币时间价值的两种基本方法,反映利率与期限因素对货币时间价值的影响。下面是讨论中将要用到的一些符号的定义:
单利是指本金不变的计息方法,复利是指每期本金加上本期的利息后再计算利息的计息方法。与单利相比,复利计算使得储蓄或投资可以从前一期的利息中获得收益。 单利的计算公式:FV=PV×(1+r×t),PV=FV/(1+r×t) 复利的计算公式:FV=PV×(1+r)t,PV=FV/(1+r)t
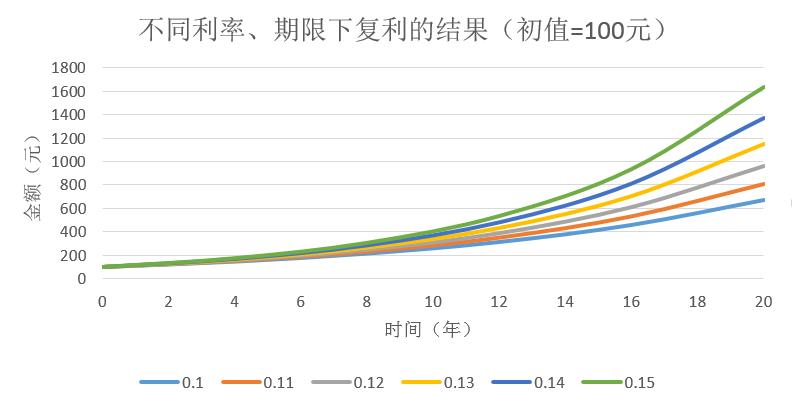
复利的威力 10,000元存款,存10年,年利率10%,10年后其价值为多少? 如果存款是单利:FV=10000×(1+10%×10)=20000元 如果存款是复利:FV=10000×(1+10%)10=25937元 二者差值:5937元 复利给我们的启示是:复利是实现投资收益加速增长的原则,复利与时间有着密切的关系,时间越长,复利的效果越显著。通过及早投资,你将有更多的时间来获取复利的收益。投资大师巴菲特在1994年的一次演讲中说,“复利有点像从山上往下滚雪球。最开始时雪球很小,但是往下滚的时间足够长(从我买入第一只股票至今,我的山坡有53年这么长),而且雪球黏得适当紧,最后雪球会很大很大。” 影响复利收益的另一个重要因素是收益率,收益率的很小变动在长期会引起投资收益的重大改变,下图描述了初始投资为100元,收益率水平相隔一个百分点时20年后的不同收益结果。同样,在长期复利中收益率降低一个百分点对收益的负面影响也是本图所表现的主题。
根据下面所列出的投资信息,计算利息(收益)和投资到期后的终值。
72法则:投资收益的速算法 72法则的含义 如果年利率为r,那么投资收益将在大约72/r年后翻一番。许多时候,投资收益的计算涉及指数,需要使用计算器,72法则可以帮助我们方便地了解一项投资的大致收益范围。
72法则的推导 FV=PV(1+r)^t,这是复利公式。令FV=2PV,即收益翻一番,则公式变为2=(1+r)t。取对数,t=ln2/ln(1+r), 当r较小时,ln(1+r)≈r,此时t≈ln2/r=0.693174/r。由于69因数少,其附近数字中72因数较多,所以通常采用72用于简化计算。 10000元存款,年利率8%,请问这项存款金额翻一番需要多少年? 通常的方法:10000×(1+8%)t=20000,t=ln2/ln1.08=9.006年 使用72法则:72÷8=9年 72法则只是一种速算方法。当利率在6%-12%之间时,使用72法则比较准确。
复利期间和有效利率 计息频率对资产累积价值的影响 若一年内对某金融资产计m次复利,则t年之后得到的价值 FV=PV×(1+r/m)(m×t ) 10000元存款,存10年,年利率10%,请问这项存款10年后的价值为多少? 1.按年计息:FV=10000×(1+10%)10=25937元 2.按季计息:FV=10000×(1+(10%)/4)(4×10)=26851元 3.按月计息:FV=10000×(1+(10%)/12)(12×10)=27070元 结论:在复利模式下,每期计息次数越多,相同资金累积的价值越大
有效年利率 有些金融资产的计息周期不等于标准年,它所提供的利率不能直接与其他按年计算的金融资产进行对比。此时,我们需要将这些金融资产的利率换算为年利率,这称为有效年利率(EAR)。 公式 FV=PV×(1+EAR)t= PV×(1+r/m)(m×t) EAR=(1+r/m)m-1 投资50万元,年利率为12%,每半年计息一次,请问有效年利率是多少?3年后其价值将变为多少? EAR=(1+(12%)/2)2-1=12.36% FV=PV×(1+EAR)3=500000×(1+12.36%)3=709260元
名义利率和实际利率 在使用利率计算投资收益时,需要注意通货膨胀因素。我们将未考虑通货膨胀时的利率称为名义利率,而将考虑通货膨胀的利率称为实际利率,实际利率能够反映投资收益的真实收益。 符号:名义利率r,实际利率i,通货膨胀率p 1+r=(1+i)(1+p) r=i+p+ip≈i+p 由上式可知,名义利率约等于真实利率与通货膨胀率之和 假如一份短期国库券的名义收益率是9%,而此时的通货膨胀率是%,那么该国库券的真实收益率是多少? 精确计算方法:i=(1+r)/(1+p)-1=(1+9%)/(1+5%)-1=3.8% 简易计算方法:i≈r-p=9%-5%=4%
现值与终值 在前面的例子中,我们都是在计算一笔投资未来的价值,也就是终值。然而很多时候我们需要倒过来计算,未来获得的一笔收入在今天的价值是多少,这称为现值。为什么要这么麻烦呢?因为货币是有时间价值的,同等数额未来货币的价值低于今天。究竟低多少?这就需要计算未来一笔收入的现值才能确定。 现值计算的步骤和复利计算方向相反。在现值计算中,我们使用的是贴现率的概念,贴现率是用于计算未来资金现值的利率,也用i表示。用于现值计算的公式是PV=FV/(1+i)n
假定5年后和10年后你将分别获得一笔10万元的收入,再假设贴现率为5%,那么这两项收入的现值为多少? PV=FV1/(1+i)n1+FV2/(1+i)n2 =10000/(1+0.05)5+10000/(1+0.05)10 =7835.26+6139.13=13974.39 从上面的计算可以看出,未来一笔收入的现值与期限和贴现率成反向的关系。贴现率越高,期限越长,现值越低。如果你将来在企业工作,你可能会经常听到贴现这个词。企业为了获得现金,常常将尚未到期的票据拿到银行贴现。银行在收取票据后,会根据票据的面值和当时的市场贴现率收取票据向企业提供现金。
年金 年金是在一定期限内,时间间隔相同、不间断、金额相等、方向相同的系列现金流。例如,你每年向某一投资账户存入一定数量的金额,这就是一种年金。假定这个投资账户的利率为r,一共存入t期,我们可以计算最终这个账户中有多少钱。由于年金的利息也要计算,所以年金终值和现值的计算通常采用复利的形式。 符号:
期初年金的终值与现值 其初年金是指现金流发生在每期期初,例如房租、养老金支出、生活费支出、教育支出、保险缴费等。下面是期初年金现值与终值的计算公式: FV_期初=C×(1+r)t+C×(1+r)(t-1)+…+C×(1+r) =C/r×[(1+r)t-1]×(1+r) PV_期初=C+C/(1+r)+C/(1+r)2 +…+C/(1+r)(t-1) =C/r×[1-(1/(1+r))t]×(1+r) 一位银行白领在每年年初存款10万元,共存10年,年利率5%,10年后可得多少钱? FV=(100000/0.05)×[(1+0.05)10-1]×(1+0.05)=1320679元 一位教师预计退休后每年生活费需要6万元,每年年初用钱,退休后的总期限预计30年,利率为5%,这位教师在退休当年应当准备多少钱? PV=(60000/0.05)×[1-(1/(1+0.05))30 ]×(1+0.05)=968464元
期末年金的终值与现值 期末年金是指现金流发生在每期期末,例如分期贷款往往在每期期末归还。下面是期末年金现值与终值的计算公式: FV_期末=C×(1+r)(t-1)+C×(1+r)(t-2)+…+C =C/r×[(1+r)t-1] 也就是说,期初年金的终值等于期末年金的终值乘以1+r。相当于期末年金复利一期。 PV_期末=C/(1+r)+C/(1+r)2 +…+C/(1+r)t =C/r×[1-(1/(1+r))t] 同样,期初年金的现值等于期末年金的现值乘以1+r。相当于期末年金复利一期。 假定上面那位银行白领决定将存款时间改在每年年末,每次存款10万元,共存10年,年利率5%,10年后可得多少钱? FV=(100000/0.05)×[(1+5%)10-1]=1257789元 再假定上面那位教师预计退休后每年生活费需要6万元,每年年末用钱,退休后的总年限预计30年,利率为5%,在退休当年应当准备多少钱? PV=(60000/0.05)×[1-(1/(1+0.05))30 ]=922347元 本页引言中的例子也可以用期末年金终值公式来求解,年金的期限分别为21年和26年,请验算例子中所给出的两个终值。如果这位投资人在每年的期初进行投资,结果会有怎样的不同?这种差别对你有何启示? |